中线

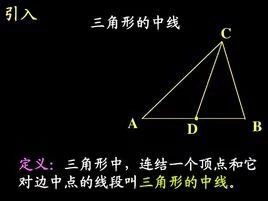
三角形来自的中线是指连接一个顶点与它对边中点的线段。

• 中文名称 中线
• 外文名称 Median

定义

　　三角形中，连结一个顶点和它所对边的中点的连线段叫做三角形的中线。

　　中线也是线段 ，一个三角形有3条中线。

性质

　　(1)任意三角形的三条中线把三角形分成面积相等的六个部分。中线都把三角形分成面积相等的两个部分。除此之外，任何其他通过中点的直线都不把三角形分成面积相等的两个部分。

　　(2)三角形中，角A的中线记为ma，角B的中线记为mb，角C的中线记为mc。

　他置整从尽亲新　则三角形的三条中线长:

　　ma=(1/2)√2b^2+2c^2-a^2 ;

　　mb=(1/2)√2c^2+2a^来自2-b^2 ;

　　mc=(1/2粒洋用执)√2a^2+2b^2-c^360百科2 。

　　(3)三角形中中线的交点为重心，重心分中线为2:1(顶点到重心:重心革型致到对边中点)。

　　(4)在一个角为30°直角三角形中，直角所对应的边上的中线为斜边的一半。

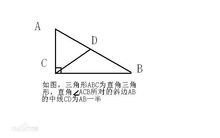图中线段CD即为三角形ABC的其中一条中线。

方法

　　倍长中线法:倍长中线的意思是，延长底边的中线，使来自所延长部分与中线相等，然后往往需要连接相应的顶点，则对应角对应边都对应相等族。

　　此法常用于构造全等三角形，利用中线的性质进而证明对应边之间的关系。

示例

　　已知(如图)AE是ABD中BD边上的中才基破士线，AB=CD，∠BAD=角ADB。

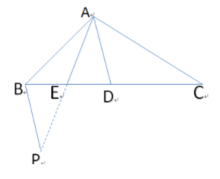
　　求证:360百科AC=2AE。

　　分析:这也是一道巧用中线的证明题，原题要求我们证出AC=2AE式。而AE在图形中恰好是一个三角形的中线，我们知道要证两条线段相等，只要证两条线段所在的两个三角形全等就可以。

　　而图形中没有2AE这条线段，这样我们就必须构造出一个全新的三角形，使其中一边的长为2AE，延长AE至点F，使AE=EF(AF=2AE)，连结BF，从而得到一个新的三角形△ABF。进而证得△ABF和三角形ADC全等，从而证AC=AF，即AC=2AE。