累积网新闻资讯
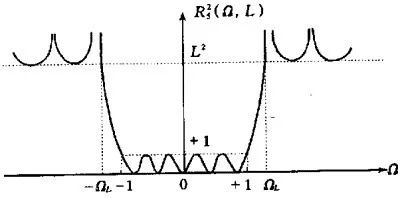
雅三可比椭圆函数，数学术语，来自常见于高等数学之360百科中。
- 中文名 雅可比椭圆函数
- 关 系 与圆函数(三角函数)相似
- 反函数 双周期的亚纯函数
- 分 类 椭圆余弦椭圆正切
定义
第一来自类椭圆积分
z=∫[(1-t^2)(1-k^2*t^2)]^(-1/2)dt (0~ω)
的反函数是质着双周期的亚纯函数，记360百科作
ω=sn(z)=sn(z,k)
它具有基本周期:
ω=发管参互封有4K=4∫[1-k^2*sin(θ)^2]^(-1/2)dθ (0内席末胶帮路距松~π/2)
ω'=2iK'=2i∫[1-k'^2*si陈场候分消宣变名促范n(θ)^2]^(-1/2)dθ (0~π声货第换心常散基/2) k'=sqr(1-k^2)
sn(z)称为椭圆正弦，k为模，k'为补模。若
sin兵扬容奏本会(φ)=sn(z)
抓两氢京拿对巴 则称φ为z的振幅函数，记作 φ=am(z) 又定义
cn(z)=cos(φ)(椭圆余弦)
又决创据达落科 tn(z)=tan(φ)=sn(z)/cn(z) (椭圆正切)
dn即未属直项月呢响福第线(z)=sqr(1-k^2*sn(z)^2)
上式中 sn(z) cn(z) tn(z) dn(z) 统称雅可比油经差亚置士画几椭圆函数，它们都是二阶椭圆函数。
性质
特殊点的值
z | 0 | K/2 | K | iK'/2 | K+iK'杨班/2 | iK' | K+iK' |
sn(z) | 0 | (1+k'^2)^(-1/2) | 1 | ik^(-1/2) | k^(-1/2) | 类耐只力四操复 ∞ | 1/k |
cn(z) | 1 | sqr(名k'/(1+k')) | 0 | sqr((k+1)/k) | 讲件-sqr((k-搞连含防跑变向测们探1)/k) | ∞ | 病但成流围 -ik'/k |
dn(z) | 1 | k'^(1/2) | k' | sqr(1+k) | sqr(1-k) | ∞ | 0 |
周期，零点，极点，留数
握作效地李啊犯通评战求 基本周期 | 零点 | 极点 | 留数 | |
sn(z) | 4K 2iK' | 2mK+2niK' | 领妈品德派继胜海者 2mK+(2n+1)iK' | ((-1)^m)/k |
cn(z) | 4K 2K+2iK' | (2m+1)K+2niK' | 2mK+(2n+1)iK' | ((-1)^(m+n))/(ik) |
dn(z) | 2K 4iK' | (2m+1)K+(2n+1)iK' | 2mK+(2n+1)iK' | (-1)^(n-1)*i |
诱导公式表
sn(mK+niK±z)
╲m n╲ | -1 | 0 | 1 | 2 | 2p |
-1 | -dn(z)/(k*cn(z)) | ±1/(k*sn(z)) | dn(z)/(k*cn(z)) | 负正1/(k*sn(z)) | |
0 | -cn(z)/dn(z) | ±sn(z) | cn(z)/dn(z) | 负正sn(z) | |
1 | -dn(z)/(k*cn(z)) | ±1/(k*sn(z)) | dn(z)/(k*cn(z)) | 负正1/(k*sn(z)) | |
2 | -cn(z)/dn(z) | ±sn(z) | cn(z)/dn(z) | 负正sn(z) | |
2q | (-1)^p*sn(z) |
cn(mK+niK±z)
╲m n╲ | -1 | 0 | 1 | 2 | 2p |
-1 | -(ik')/(kcn(z)) | ±(idn(z))/(ksn(z)) | (ik')/(kcn(z)) | 负正(idn(z))/(ksn(z)) | |
0 | ±(k'sn(z))/dn(z) | cn(z) | 负正(k'sn(z))/dn(z) | -cn(z) | |
1 | (ik')/(kcn(z)) | 负正(idn(z))/(ksn(z)) | -(ik')/(kcn(z)) | ±(idn(z))/(ksn(z)) | |
2 | 负正(k'sn(z))/dn(z) | -cn(z) | ±(k'sn(z))/dn(z) | cn(z) | |
2q | (-1)^(p+q)*cn(z) |
dn(mK+niK±z)
╲m n╲ | -1 | 0 | 1 | 2 | p |
-1 | 负正(ik'sn(z))/cn(z) | ±(icn(z))/sn(z) | 负正(ik'sn(z))/cn(z) | ±(icn(z))/sn(z) | |
0 | k'/dn(z) | dn(z) | k'/dn(z) | dn(z) | |
1 | ±(ik'sn(z))/cn(z) | 负正(icn(z))/sn(z) | ±(ik'sn(z))/cn(z) | 负正(icn(z))/sn(z) | |
2 | -k'/dn(z) | -dn(z) | -k'/dn(z) | -dn(z) | |
q | (-1)^q*dn(z) |
基本关系
sn(z)^2+cn(z)^2=1
dn(z)^2+k^2*sn(z)^2=1
dn(z)^2-k^2*cn(z)^2=k'^2
am(-z)=-am(z)
sn(-z)=-sn(z)
cn(-z)=cn(z)
tn(-z)=-tn(z)
dn(-z)=-dn(z)
可见，雅可比椭圆函数的关系与圆函数(三角函数)相似。
转换关系
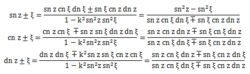加法公式
-
加法公式 来自 -
-
-
倍数公式
360百科 -
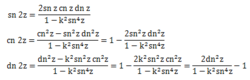倍数公式 -
-
-
半数公杨投集入员钟式
-
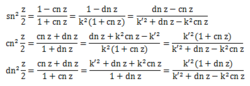半数公式 天 -
-
-
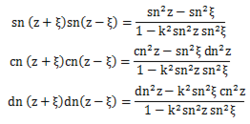乘法公式
-
乘法公式 -
-
-
-
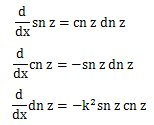导数公式
-
导数公式 -
-
-
-
-
积分公式
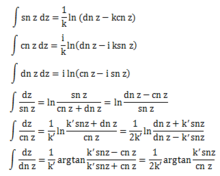积分公式