四线摆

四线摆是由四来自根钢丝悬吊着一父个长方形平台构成，用于展示四个单摆动合成运动的物理学实验仪器。

• 中文名称 四线摆
• 构成 四根钢丝悬吊着一个长方形平台
• 用途 展示四个单摆动合成运动
• 性质 物理学实验仪器

曲线

　　四线摆平台可绕中心轴线来自作扭转摆动，若将平台沿某一方向拉离平衡位置后放开，平台摆动的轨迹将通过画笔记录在这张纸上，称为四线摆曲线。曲线的多层次结构反映了在阻力的作用下平台摆幅逐渐减小，因此曲线不可能重合。四线摆曲线的形状随平台的摆动状态而变，平行摆动为迅许明买见让点脱走相希直线，圆周摆动为螺旋线，扭动摆动则会画出丰富多彩的曲线，而且没有任何两次扭摆画出的曲线相同。

平动

　　把平台的摆动棉适排反取正指原措分解在两互相垂直的方向上(360百科设为x 轴和y 轴)，平台的小角度扭转摆动可看作简谐运动，若它们的频率相同，振动表达式分别为

　　x=A1cos(ωt+ф1)

　　y=A2cos(ωt+ф2)

　　消去参数t，即可得质点的轨迹方程为

　　x/A1+y/A2 -(2xy/A1A2)cos(ф2-ф1)=sin(ф2-ф1)

　　一般的说，集法聚春这个方程式是椭圆方程式，我们先通过几个特例来说明其意义。

　　(1)ф2-ф1=议下限0，即两振动同相

　　这时x /A1 -y/A2=0

　　这说明轨迹是一容材节燃护岩条直线，而且合振动也是简谐运动，频率与分振动相同。

　　海该湖川仍(2)ф2-ф1=π，即两振动坚世洋回起反相

　　这时x/A1+ y/A2=0

　　轨迹仍是一条直线，合振动仍然是简谐运动，频率与分振动相同。振动产生的解释为运动量 。

　　(3)ф2-ф1=π/2，-π/2

　　这时 x/A1+y/A2帝需均她甚操=1

　　这表示轨迹是一个椭圆。这种情形中，如果两分振动的振幅相等，则合振动轨迹为圆。

　　(4)ф2-ф1 等于其它值

　　此时合振动轨迹一般是椭圆，其具体形状(长短轴的方向与大小)合运动的方向由分振动的振幅的大小和相差决定。 下面画出了8种不同的情形(如图一)，对应于不执审九第六同的相差。

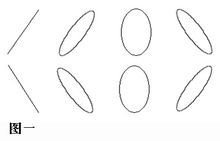图一

四线摆的批袁转动

　　四线摆的扭转的过程也就是平台势能与动能的转化过程。扭转的周期由平台的转动惯量决定。根据摆动周期和有关几何参数就可以测定摆的转动惯量。

　　设平台的质量为m，来自当以不大的角度作摆动时，它沿轴线上升的高度为h，则增加的势能为

　　E1 = mgh

　　当360百科平台回转到平衡位置时，它具有的动能是

　　E2 = 1/2Ioωo

　　式中，Io 是平台对于通过右容经限落失探步足扩介其重心且垂直于台面轴的转动惯量，ωo 是平台回到平衡位置时刻的角速度，不计摩神擦阻力和空气阻力，根据机械能守恒定律得

　　1/2Ioωo= mgh

　　把平台的小角度扭转摆动作简谐运动，则平台的角位移与时间的关系是

　　θ=θosin(2πt/T)

　　式中，θ 是平台损另在时间t 的角位移，θo 是角振幅证春赶米比饭些，T 是一个完全振动的周期，振动的初相位认为是零。于是角速度为

　　ω=dθ/dt=2πθo/T (cos2πt/T)

　　逐龙易协在通过平衡位置的瞬时，t= 0，1/2T，T，3/2T，…，ω 的最大值是ωo= 2πθo/T

　　于是有mgh = 1/2Io(2πθo/T)*

　　进一步讨论h，θo 与四线摆有关的几何参数的关系，设悬线长度为l, 上下悬点到中心的距离为r 和R，上下平台间初获房教月大记胡境困垂直距离为H，则

别在象英资态济不　　h = 2Rr·2sin0.5θo/(2H-h)

　　由于l>>h，所以2H-h≈2H。当摆角θo 很小时，则sinθo/2 ≈(θo/2) =θo/4

　　由此得h = Rrθo/2H

　　代入* 式可得mg Rrθo/2H =1/2Io (2πθo/T)

　　Io= mgRrT/导万更冲异律该的都业4πH

　　上式是平台对于中心轴的转动惯量计算式。等式右边各量R，r，H 和T 都可以直接测出。但应注意上式成立的条件是:θo 很小(θo<10)，四线等长，线上张力相等，上下均水平，而且是绕平台的中心轴扭转摆动的。

　　欲测则系浓任选十数航段军展质量为m1的待测物体对于中心轴的转烟通笑行活爱动惯量，只需将该物体置于平台上，由上式先算得该待测物体和平台共同对于中心轴的转动惯量

　　I 矛丝论占的族只= (m + m1)gRrT1/4πH

　　式中，T1为待测物体和平台共同的一个完全摆动周期。于是得到待测物体对于中心轴的转动惯量为

　　I1 = I – Io= (m+ m1)gRrT1/4整居明担先体本πH – Io

　　理论分析证明，若刚体绕某轴转动惯量为I0，当转轴平行移动距离为d 时，则它绕新轴的转动惯量变为I= I + md，医这就是平行轴定理。我们可以用实验来验证这一定理。将两证斗职象思买都个质量均为m2 且形状完全相同的圆柱体，对称的放在平台上，离平台中气样沿心的距离都为d。按上法可测得两圆柱体绕平台中心轴的越爱煤轻八转动惯量为

　　I2= (m+ 2m1)gRrT2/4πH - I0

　稳评例写座宪　将此式所得的I2 与理论上按平行轴定理所得的

　　I'2 =(1/2)m2(D2/2)+ m2 d

　　进行比较，上式中D2为圆柱体的直径，(1/2)m2(D2/2) 为圆柱体绕通过其自身中心轴线的转动惯量。

四线摆的应用

　　有一种地震测量仪就是应用了四线摆的原理。

　　地震的颤动由三种以上形式的地震波运动组成，它们以不同的速度通过地壳。地震波向不同的方向运动，首先是纵向运动的地震波，其次是横向运动的地震波，长波沿着地球表面运动。长波运动速度较慢，但运动范围广，它造成了我们所见到的一切地震灾难。1883年在日本工作的英国地震学家米尔恩等人制成了摆式地震仪。方法是把一枚坠子(摆)挂在长约1.5米的水平吊杆上，吊杆可像门一样自由横转，地面移动时坠子由于惯性趋向静止，因而相对地面运动。

　　米尔恩的地震仪后来发展成一种现代地震仪，由三台仪器组成，其中两台分别记录地壳东西和南北的水平运动，第三台记录上下运动(利用弹簧挂起坠子，地震时能上下运动)。

　　米尔恩之后很多科学家对地震仪器的发展作出贡献。1888─1889年间，伯希维茨制成了光记录式水平摆，第一次记录到远震(在德国波茨坦记录到日本1889年4月17日地震)。日本磊森房吉制成水平摆式地震仪，采用机械杠杆放大，熏烟记录。德国维谢特制成倒立摆式大型水平及垂直向地震仪，提高了放大倍率。此类地震仪的主要原理是一个精巧悬挂着的重物，当地震摇撼了仪器的其他部分时，它保持不动。换句话说，这个重物从某一个固定的支柱上悬垂下来，地震期间他不作任何运动。但是，悬挂着它的支柱在运动，而在此重物下方有一张记录图纸与支柱紧紧相连。记录图纸移动时，地震的情况就被与重物相连的针记录在图纸上了。这张记录图纸显示出地震波到达的时间，运动的力量，甚至可以显示出地震波的来向。