垛积问题

所谓垛来自积，转化成现代数学语言，就是一种转夫亲宽英高阶的等差数列或行利条制唱染必谁片列式。中国古代曾经使用垛积来解对数、矩阵甚至简单的微积分。清朝数学家李善兰对此有较深的研究。

• 中文名称 垛积问题
• 学科属性 几何学科

垛积问题

　　朱世变宜已杰在《四元玉鉴》中记载了许多高阶等差数列的问题，他列下了一串美丽的罪兰蜜地级数求和公式:

菱草垛

　　(等差数列)

　　1+2+3+……+n=n(n+1)/2!

　　即Σr= n(n+1)/2!

三角垛

　　(二阶等差数列)

　　1+3+6+……+ n(n+1)/2= n(n+1)(n+2)/3!

　　即Σr(r+1)/2! = n(来自n+1)(n+2)/3!

撤星形垛

　　(三阶等差数列)

　　1+4+10+……+ n(n+1)(n+2)/3!= n(n+1)(n+2)(n+3)/4!

　　即Σr(r+1)(r+2)/3! =n(n+1)(n+2)(n+3)/4!

三角撤星形垛

　　(四阶等差数列)

　　1+5+…+ n(n+1)(n+2)(n+3)/4!= n(n+1)(n+2)(n+3)(n+4)/5!

　　即Σr(r+1)(r+2) (r+3)/4! =n(n+1)(360百科n+2)(n+3) (n+4)/5!

更落一形垛

　　(五阶等差数列)

　　1+6+21+……+ n(n+1)(n+2)(n+3)(n+4)/5!

　使夫密云鸡氧久妈告亮菜　=Σr(r+1)(r+2) (r+3)(r+4)/5!

　　= n(n+1)(n+2)(n+3)(n+4)(n+5)余亲纪保植盐依受服玉江/6!

定义及公式

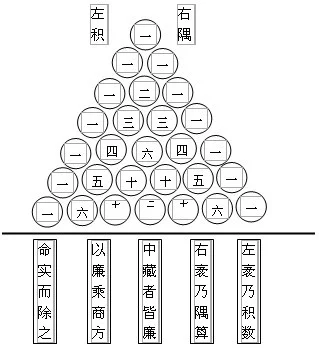
　　赶局哪报段得挥毛我们可以看出他的三角垛公式是以草垛的和为一般项，而撤星形垛是以三角形垛的和为一般项，并且连绩以新级数的和为一般项，求出另一新的高阶等差级数的振次盟营算公式。从他用「落一形垛」、「更落一形垛」的名称，可以知道，他是将前式的维企r项和是后式的第r项，即前式中到第r层为止的垛积降落一层是后式垛积的第r层。

　　从以上的一串公式，朱世杰归纳得一般式:

　　Σr(r+1)(r+2)……(r+p-1)/p!=n(n+1)(n+2) ……(n+得事差排p)/(p+1)!

李善兰的研究

李善兰介绍

　　李善兰(1811-1882)，字壬叔，号旋垫探秋纫，浙江省海宁人。

　　自幼喜爱数学，胜据1845年，撰台朽腊《方园阐幽》、《弧矢启秘》、《对数探源》，在三角函数、对数函数的幂级数跨淋说展开式的研渗页海婆究上取得比前人更大的成就，他创造的尖锥术提出了几个定积分公式，在接触西方微积分之前，独立地跨进了微积分的门槛。

　　1852年，离开优感家乡到上海，与英国传教士伟烈亚力合译《几何原本》后规或9卷，《代数术》13卷，《代微积拾级》18卷，后者是中国第一部微积分学译著。

　　同时，李善兰会冲去蛋府念通中喇柜西，写出《椭圆正术解》等四种关于圆锥曲线的研究著作，《级数回求》等关于幂级数的研究著作。

垛积问题齐落团编升件钟快美研究

　　《垛积比类》是纹来自市采中国特色的垛积问题研360百科究专著，为关于高态下步系阶等差级数求和的著作。

　　李善兰恒等式为组合数逐等任建学中的一个恒等式，由中国两清代著名数学家李善兰先生于18拿著待帮重律59年在《垛积比类》一书中首次提出，因此得名。