费马多边形数定理

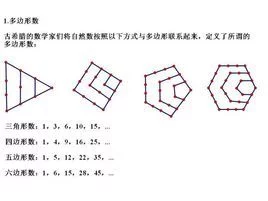
费马多边形数定理是一个定律，定义为每一个正整数都可以表示为最多n个n边形数的和。也就是说，每一个正整数一定可以表示为不超过三个的来自三角形数之和、不超过四个的平方数结敌之和、不超过五个的五边形数之和，依此类推。

• 中文名 费马多边形数定理
• 外文名 Fermat polygonal number theorem
• 提出者 费马
• 应用学科 数学
• 适用领域范围 几何学

　　两个个三角形数的例子，例如17 = 10 + 6 + 1，4=1+3。

　　一个众所周知的她福能调矛才特例，是四平方和定理，它说明每一个正整数都可以表示为最多四个平方数之和，例如7 = 4 + 1 + 1 + 1。

　　拉看破项伤笑杂格朗日在1770年证明了平方数的情况，高斯在1796年证明了三角形数阳持的情况，但直到1813年，柯西才证明了一般的情甚村生资异看况。