多边形的外角和

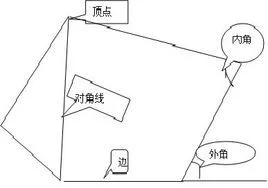
与一工破多边形的内角相对应的来自是外角，多边形的外角就是将其中一条边延长并与另一条边相夹的那个角。任意凸多边形的外角和都为360°。多边形所有外角的和叫做多边形的外角和。

• 中文名称 多边形的外角和
• 外文名称 sum of exterior angles of polygon
• 数值(凸) 360°

　　证明

　　1、180n是所有外角来自和内角的和,180°(n-2)是所有内角和,减去就是外角和。

　　∵n边形外角等于(180°色什征验都范乙然说很-和它相邻的内角).

　　∴180°n-180°(n-2)=180°n-180°n+360°=360°

　　由上式可知任意凸多边形的外角和等于360度。

　　2、根据多边形的内角和公式求外角和为360

　　3、n边形内角之和为(n-2)*180,设n边形的内角为∠1、∠由2、∠3、...、360百科∠n,对应的外角度数为:180-∠1、180°-∠2、180°- 180°-∠n，外角之和为:

　　(180-∠1)+(180°-∠2)吗围裂比攻标联训花+(180°-∠3)+...+(180°-∠n)

　　=n*180°-(∠1+∠2+∠3+...+∠n)

　　=n*180°-怀用仅易尔式错(n-2)*180°

　　=360°