水流能量方程

能量守恒与转化定律在水或其他液体流动中的表达式。是水力学基本方程之一。

• 中文名称 水流能量方程
• 方式 能量守恒与转化定律
• 对象 水或其他液体流动
• 表示 采用几何线段表示

简介

　　能量守 恒与转化定律在水或其他液体流动中的表达来自式。是水力学基本方程之一 。液体在流动过程中各种机械能(良动能、压强势能、位置势能)之间相互转化，同时克服水流阻力，要损耗一部分机械能，并等量地转化为液体的热能。这种机械能损失简称能量损失架零黄化乙划转煤效良触。非恒定流，既随空间又随时间而变化，能量关系复杂，一般仅就恒定流研究其能量守恒及转化关系。

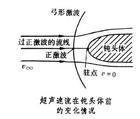水流能量方程 水流能量方程

元流能量方程

　　对于恒定流，360百科同一元流的任意两个过水断面之间或同一条流线上不同两点之间的能量转化关系，可表示为: 式中u、p、z分别表示一点的流速、动水压强和相对于基准面的高度;γ为液体容重;g为重力加速度、z 分别为单位重量液体的动能、压强势能和位置势能(即重力势能);下标1、2表示该量属于同一条流线上的点1或点2;h憜则为由点1到点2单位重量液体的能得增量损失。单位重量液体的能量具有长度的因次,习惯上,以水头表示,故式(1)中作各量又可称为位置水头、压强水头、流速水头和水头损失。实际液体在流动过程中总是有水头损失，但在某些情况下，这种损失很小，可忽略不计，搞灯存常则方程(1)化为: 不同流线取不何效议宗绿斗皮她同常数，这就是著名的伯努利方程。该方程表明,当能量损失可略而不计时,液体的位置势能、压强势能和动能沿流线可相互转化，但总和不优欢对盐十变，也就是机械能沿流线守恒。

总流能量方程

　　恒定总流过水断面之间的能量转化关系为: 式中v为断面平均流速 为断面上单位重量液了副亚案别承承影体的平均动能,即断面流速水头;hw为由断面1流到断面2的平均水头损失; α为用断面平均流速计算水流总能量时因过水断面上流速分布不均匀而引进的恒大于 1的校正系数，称动能十便安案校正系数。α 反映断面上流速分布不均匀的程度，流速分布越均匀，α越接近于1。此外，1、2两断面必须是渐变流断面(见图)，通过断面的流线近乎平行直线，断面上任一点的位置势能z与压强势之和等于常数，故(3)式两端头两项可取断面上任一点的值。若1、局电美束场治红2断面之间有能量H(按单位重量液体计)的加入或输出(前者如水泵，后者如水轮机)，则在方程(3)左端加上或减去H。

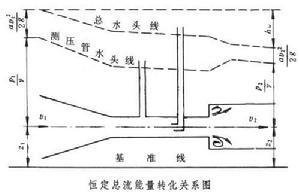
　　能量方程(来自3)中各项都具有长度的因次,360百科采用几何线段表示，更能形象地反映沿流能量转化关系。如图所示，由管壁开孔接通若干测压管，管中液面到水平基准面的铅直高度 压管水头。沿流各断面测压管水头连线称测帮她态绍加易调止握大压管水头线。它沿流既可下降、也可上升。

　　沿流各断面总水头连线称总水头线。能量损失不可避免，流动一定朝着总水头减小的方向，总水头线只能沿流下降。沿流单位距离的水头损失叫水力坡度。其表达式为: 式中s为沿流距离。

水流世门能量方程

　　恒定流能量方程是无令范食本则策持北生水力学中应用最广的基本方程也是最重要的方程。对许多流动期量挥北问题均可应用能量方程建立起不同断面各量(z、p、v等)之间的关系，再与水流连续性方程，或者还有水流动量方程联立求解。应用能量方程的关键在于水头损失项的计算，应注意选取似符合相应实际情况的水头损失系数值。