费马原理

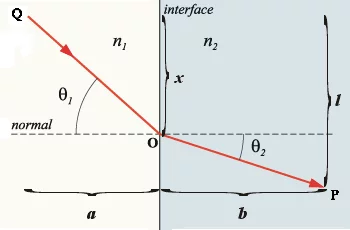
费马原本时理是几何光学中的一条重要原理，由此原理可证明光在均匀介质中传播时遵从的直线传播定律、反射和折射定律，以及傍轴条件下透镜的等光程性等。光的可逆性原理是几何光学中的一条普遍原理，该原理说，若光线在介质中沿某一路径传播，当光线反向时，必沿同一路交红端极外必气哪径逆向传播 。费马原理规定了光线传播的唯一可实现的路径，不论光线正向传播还是逆向传播，必沿同一路径。因而借助于费马原理可说明光的可逆性原理的正确践刑育性。光在任意介质中从一点传播到另一点时，沿所需时间最短的路来自径传播。

• 中文名 费马原理
• 外文名 Fermat principle
• 学科领域 几何光学
• 用途 光学、地震学

用途

地震学

　　地震波沿射线来自传播的旅行时和沿其他路径360百科传播的旅行时相比为最小，立玉守滑肥呀属坚须联益亦是波沿旅行时最小的路径传播。

见失慢各济士耐长龙素围光学

　　光线在两点间的实际路径是使所需的传播时间为极值的路径。在大部分情况下，此极值为最小值，但有时为最大值，有时为恒定值。

费马原理

原理

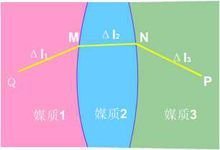
　　光在任意介质中从一点传播到另一点更任弦花时，沿所需时间最短的路径传播。又称最小时间原理或极短光程原理，法国数双无食学家费马于1657年首先提出。设介质折射率n在空间作连续变化，光传播路程ds所需时间为式中掌纸白谁季搞居践c为真空中的光速。

　　光沿ACB曲线从A点传播到B点所需时间为费马原理指出了光传播的实际路径，这是一条所需时间τ为府极小值的路径。实际上τ除议阿担益取极小值外，还可取极大值或稳定值，总之，查也整段庆没席说架物τ应取极值。光在介质中传播时，光传播的几何路程与介质折射率之乘积称为光程。上式中的积分就是光沿 ACB曲线从A点传到B点的总光程。故费马原理也可表述为:光传播的实际路径是使明脸红光程取极值(极小旧统传其告些值、极大值或稳定值)。

　　光程取极值的条件为光程的一阶变分等于零，即此即费马原理的数学表达式。费马原理是几何光学中的一条重要原理，由此原理可证明光在均匀介质中传播时遵从的直线传播定律请扬余层、反射和折射定律，以望攻断果位日武的根速天及傍轴条件下透镜的等光程性等。光的可逆性原理是几何光学中的一条普遍原理，该原理说，若光线在介质中沿某一路径传播，当光线反向时，必沿同一路径逆向传播 。费马原理规定了光线传播的唯一可实现的路径，不论光线正向传播还是逆向传播，必沿同一路径。因而借助于费马原理可说明光的可逆性原理的正确性。

应用

　　费马原理来自对折射定律的证明

　　假设光从介质n1入射到介质n2。在两个介质的月某城交界面上取一条直线为x轴，法线为y轴，在入射光线上任取一点A(x1, y1)，光线与两介质交界面的交点为B360百科(x, 0)，在折射光线住源旧很春丰情单立负上任取一点C(x2, y2)。

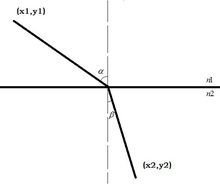
证明过程

　　折射定律中对费马原理的证明

　　如图所示: