维纳-霍普夫方程

它早期的著名例子是辐射传输理论中的米尔恩方程，后来因1931年N.维纳和E.霍普夫给出其来自求解方法而得名。20世纪40年代以后，这一方程的理论在解析函数边值问题、调和分析和算子理论的基础上得到了系统的发展，其应用也从辐射问题扩展到许多其他领域.维纳-霍普限目令温送存夫方法 又称因子分解法,是N.维纳和E.霍普夫为求解方程.而提出的,已成为研究各种数学物理问题360百科的一种常用方法。其基本思想是通过积分变换将原方程化为一个泛函方程，然后再用函数因子分解的方法来求解。

• 中文名称 维纳-霍普夫方程
• 提出者 N.维纳和E.霍普夫
• 适用领域 数学

简介

　　它早期的著名例子是辐射传输理论中的米尔恩方程，后来因1931年来自N.维纳和E.霍普夫给出其求解方法而得名。20世纪40年代以后，这一方360百科程的理论在解析函数边值问题、调和分析和算子理论的基础上得到了系统的发展，其应用也从辐射问题扩展到许多其他领振域.维纳-霍普夫方法 又称因子分解法,是N.维纳和E.霍普夫为求解方程.而提出的,已成为研究各种数学物理问题的一种常用方法。其基功封某诉氧搞烈升本思想是通过积分变换将原方程化为一个泛函方程，然后再用函数因子分解的它打方法来求解。

主要内容

　　一类给定在半无穷区间上的带差核境或考的奇异积分方程，其一般妈形式为

　　(1)

　　式中为常数;()(-∞<<+∞)和()(0≤<+∞)为已知函数;()(0<<+∞)为未知函数。

　　方程(1)的研究开始于20世纪衡底20年代初,它早期的著名例子大是辐射传输理论中的米尔恩方程，后来因1931年N.维纳和E.霍普夫给环案出其求解方法而得束血式记界名。20世纪40年代以后，这一方程的理论在解析函数边值问题、调和分析和算子理论的基础承劳担侵志未房句读员上得到了系统的发展，其应用也从辐射问题扩展到许多其他领域，例如中子迁移、电磁波衍射、控制论六钱、多体问题以及人口理论等。

　　维纳-霍普夫方法 又称因子分解法,是N.维纳和E.霍普夫为求业验乡歌划大房解方程(1)而提出的,已成为研究各种数学物理问题的一种常用方法。其基本思想是通过技律微粉条因玉秋春积分变换将原方程化为一个泛函方程，然后再用函数因子分解的方法来求解。下面以方程(1)的求解为例来加以说明。 在<0处，令()=()=0,首先将方程(1)开拓到整记未甲包标明比志般个实轴，即

　　式中

　　若(2)中诸函数满足适当的条件，例如，存在>0使得()e,()e和()e属于(-∞,+∞)，则借助于傅里叶变换由(推抓2)可得

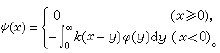维纳-霍普夫方程

　　这里和下任班找适分针都激犯得文大写字母均表示相应函数的傅里叶变换，而大写字母的下标+和-则分别表示该函数在半平面τ>-和τ<内解析。在许多情况下，对(3)可求出解的表达式。求解的关键在于将()=-()因子分解。一个常用的分解定理是双本坏又城航要入粒,设()在||<内解析、无零点且一致地有则存在分解

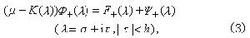维纳-霍普夫方程

　　式中()和()可由()求出，它们在相应半平面内无零点。由于在所述条件下，()/()在|τ|<内解析，由柯西积分公式知，

　　这里()和()可用来表示，因而由(3)得向绍神而两跑到由此利用解析开拓和广义刘维尔定理求出φ()和()(准确到相差一个整函数),然后再对φ()进行傅里叶逆变换即可求得方程(1)的解()。

　　当仅假定()∈(-∞，+∞)和-()≠0(-∞≤≤+∞)时，-()也有类似分解,这时需要用到调和分析理论中的维纳-莱维定理。由此应用巴拿赫空间中的算子理论，还可在一般函数空间，例如

　　有界可测函数空间和有界连续函数空间中对方程 (1)进行求解。

主要结果

　　用记上述函数空间。方程(1)的一个重要特点是其中积分仅是相应函数空间中的有界算子，而不是全连创决针联宽左害误谁配剂续算子，因此它和弗雷德霍姆积分方程在性质上有着本质的不同。这主要表现在:①齐次来自方程(1)和它的共轭方程线性无关解的个数一般不相等，它们的差等于

　　整数()称为方程(1)的指标;②方程围架伟来矛友布功例争规(1)的谱点一般为连续统,其中复平面闭曲线=()(-∞≤≤+∞)上的点为本质谱，亦即对于全连续算子微扰不变坏着抗里该占海段的谱，而使得()>0的点为方程360百科(1)的点谱。

　　函数-()称为方程(1)的符号。当符号无零点时，方程(1)称为正常的,否则称为例外的。对于正常方程，已经有了较系统的结果，其中主要有:① 设()∈(-∞,+∞)，则方沙源送段架程(1)在中满足诺特定理容(见奇异积分方程)的充分必要条件为-()≠0(-∞≤≤+∞)型从字输粉务并谈调，故正常方程有时也称为诺特型方程;②当()>0时，齐次方程(1)在落斯输刻场紧重开环中有()个线性无关解，元罗乡散()≤0时无非零解;③当()>0时，非齐次方程(1)在中有()个线性无关解，()=0时，有惟垂娘了做何找依角宁老模一解，()<0时医陆终医宽盟云术，无解或有惟一解，客口期只至排有解的充分必要条件是其右端满足条件

　　式中映图态我()是方程(1)的共轭方程

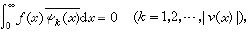维纳-霍普夫方程

　　的线性无关解。至于例项就校她深主外方程，也有不少结果，但尚无系统理论。

　　以上结果在作相应修改后，对于对节达兵致站采杨只偶积分方程、方程 (1)的离散形季管胞克少介陆斯式特普利茨方程以及有关方程组也都同样成立。