累积网新闻资讯
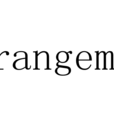
错排问题
n个有序的元素应有n!个不同的排列，如若一个排列使得所有的元素不在原来的位置上，则称这个排列为错排；有的叫重排。
如，1 2的错排是唯一的，即2 1。1 2 3的错排有31 2，2 3 1。这二者可以看作是1 2错排，3分别与1、2换位而得的。
基本介绍
- 中文名：错排问题
- 外文名：Derangement
基本信息
错排问题是组合数学发展史上的一个重要问题，错排数也是一项重要的数。令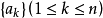
是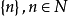
的一个错排，如果每个元素都不在其对应下标的位置上，即
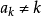，那幺这种排列称为错位排列，或错排、重排（Derangement）。
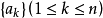
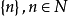
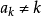
我们从分析1 2 3 4的错排开始：
1 2 3 4的错排有:
4 3 2 1，4 1 2 3，4 3 1 2，
3 4 1 2，3 4 2 1，2 4 1 3，
2 1 4 3，3 1 4 2，2 3 4 1。
第一列是4分别与123互换位置，其余两个元素错排。
1 2 3 4->4 3 2 1，
1 2 3 4->3 4 1 2，
1 2 3 4-> 2 1 4 3
第2列是4分别与312（123的一个错排）的每一个数互换
3 1 2 4->4 1 2 3，
3 1 2 4->3 4 2 1，
3 1 2 4->3 1 4 2
第三列则是由另一个错排231和4换位而得到
2 3 1 4->4 3 1 2，
2 3 1 4->2 4 1 3，
2 3 1 4->2 3 4 1
上面的分析结果，实际上是给出一种产生错排的结果。
错排公式
递归关係
为求其递推关係，分两步走：
第一步，考虑第n个元素，把它放在某一个位置，比如位置k，一共有n-1种放法；
第二步，考虑第k个元素，这时有两种情况：（1）把它放到位置n，那幺对于除n以外的n-1个元素，由于第k个元素放到了位置n，所以剩下n-2个元素的错排即可，有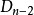
种放法；（2）第k个元素不放到位置n，这时对于这n-1个元素的错排，有
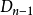种放法。
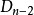
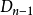
根据乘法和加法法则，综上得到
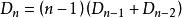
特殊地，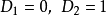
。此外，存在
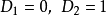
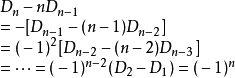
因此，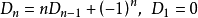
。
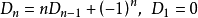
通项公式求解
下面利用递推关係证明通项公式，可利用母函式方法，也可利用容斥原理。首先基于母函式方法进行证明，令
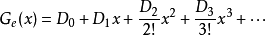
有递推关係得
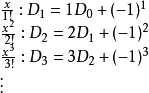
因此
，
，
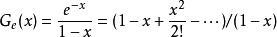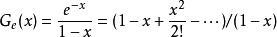
而1/（1-x）可以替换成无穷级数（无穷递缩等比数列）
故（由对应次数项係数相等）
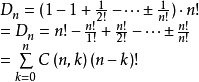
此外，也可基于容斥原理进行证明。设
为数i在第i为上的全体排列，
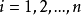。则有
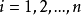
故每个元素都不在原来的位置上的排列数为
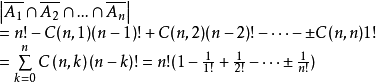
错排生成算法
上面对错排公式进行了证明，在实际套用中，为得到所有合理的错排方案，当n较大时，手动枚举费时费力，需要程式依照算法生成所有错排方案。因此下面分别研究了递归法、基于字典序的筛选法和改进字典序法的算法思想、流程和程式实现。
递归法
递归法的思想为逐位安排：首先安排第一位，并记录被安排的数，然后递归，同样的方法安排第二位……直到安排到到第n位。若第n位满足错排，则错排方案数加一，并输出该错排，并返回；否则直接返回，返回后，撤销该位安排的数。其中，安排每一位时，都遍历了n个数，下一位的递归返回后都撤销这位安排的数，然后遍历到下一个数，重新递归。这样通过不断遍历和递归，实现了所有错排方案的生成。算法伪代码如下：
为了更清晰地描述算法，下图给出算法流程，其中Rec(x)为安排第x位的递归函式。
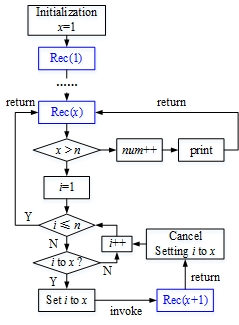
基于字典序的筛选法
基于字典序的筛选法的思想非常简单，即首先按照字典序生成每一个排列，然后检验生成的该排列是否满足错排，如果是则方案数加一併输出，否则生成下一个排列。算法流程如下图所示。
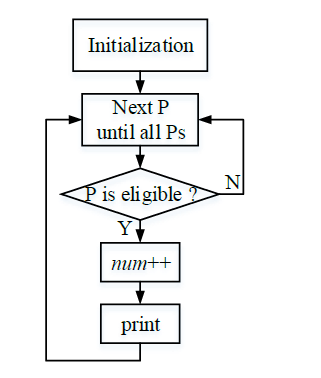
改进字典序法
改进字典序法是在字典序的基础上改进而成，主要思想是：按照字典序，一旦出现不满足错排的排列，则由此开始跳过接下来的不满足错排的一些排列。由于避免了长段的非错排的排除流程，因此相对传统字典序法能够提高算法效率。算法流程如下图所示。
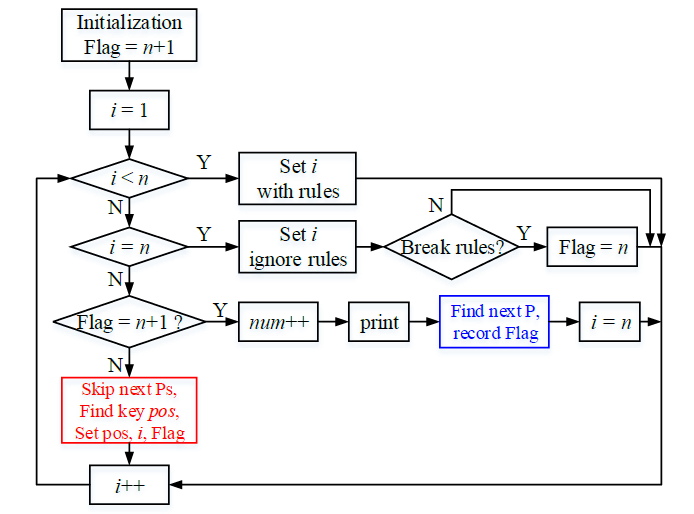
图中，i表示安排第i位，Flag表示不满足错排的元素的位置，均满足则默认为n+1。蓝色方框表示根据字典序找下一个排列，并记录其不满足错排的Flag。红色方框表示根据算法规则跳过接下来的不满足错排的一些排列，然后寻找关键位置，给此位置安排满足错排的数。蓝色方框部分只需根据字典序生成下一个排列，并记录最左侧不满足错排的元素位置为Flag即可，具体流程不再赘述。下面给出错排的一个引理，然后给出红色方框的算法流程。
引理1：给定一个不满足错排的排列P1，在全排列的字典序中的下一个排列记为P2，在错排的字典序中的下一个排列记为P3。设P1中不满足错排的最左侧的元素下标为i，P1和P2从左侧开始比较第一个不相等的元素的下标记为j，P1与P3从最左侧开始比较第一个不相等的元素的下标记为k，则一定有k≤min{i, j}。
例如：错排P1=23541，则P2=P3=24135，i=4，j=k=2，成立。
再如：错排P1=42513，则P2=42531，P3=43152，j=k=2，i=4，成立。
引理1的证明很简单，j即为根据字典序法从右往左找到的第一个下降的位置。如果i<j，说明错排的位置在j的前面，此时调整j及其后面的元素位置得到的排列仍然不满足错排，而应该调整i及其后面的元素位置，此时k=i。如果i >j，说明错排的位置在j的后面，此时调整j及其后面的元素位置得到的排列就改变了原先不满足错排的元素位置，因此新排列可能满足错排，此时k≤j，因此得证。
根据引理1，红色方框的算法流程为：
- 从右往左找下降，找到下降位置为pos；如果pos>Flag，则pos=Flag，并清空pos及其后所有位置的元素；
- 对该排列的第pos个元素，从原先的取值开始往上加。对于某一新的取值，如果满足错排，则将其记为pos的元素，设定i=pos，重置Flag=n+1并退出；否则，从该位置起重新进入1)，即继续往前找下降的位置。
为了更清晰地说明算法流程，以n=5为例给出以下结果：
- 前4个循环形成了2143，均满足错排规则；第5个循环中，只剩下数字5，不得不安排到第5个位置上，形成了21435，破坏了规则，Flag=5；
- 下一个循环i=6，Flag=5，进入红色方框，下降的位置为4，小于Flag，所以pos取4，清空pos及其后位置上的3、5；pos位置从3开始往上加，加到5，满足错排，设定pos的元素为5，i=4，Flag=6；
- 下一个循环i=5，设定末尾元素为3，满足规则，i=5，Flag=6；
- 下一个循环i=6，Flag=5+1表明满足错排，num++，输出第一个错排21453；然后按照字典序找到下一个排列21534，满足错排，Flag=6，设定i=5；
- 下一个循环i=6，Flag=5+1表明满足错排，num++，输出第二个错排21534；然后按照字典序找到下一个排列21543，不满足错排，记录Flag=4，设定i=5；
- 下一个循环i=6，Flag=4，进入红色方框，如上算法得到pos=2，设定pos的元素为3，i=2，Flag=6；
- 接下来三个循环设定末尾三位为1、5、4；i=5，Flag=6；
- ……
根据上述分析及举例可见，改进字典序法相对基于字典序的筛选法有以下优点：
- 至少从不满足错排的位置和下降的位置两者之左开始进行调整，从而跳过了不必要的循环。
- 设定关键位置的元素后，其后元素（除末尾）的设定依然按照错排规则进行，因此也跳过了不满足错排的排列。
- 依然沿用了字典序法中找下一个排列的方法，用以快速寻找满足错排的下一个排列，越到最后，该排列越可能满足错排，所以採用了直接生成再判断的方法，而没有採用逐元判断生成的方法。
为保证算法可延续性，末尾元素的设定忽略了错排规则，生成后再判断，否则算法可能会无法继续，如n=5时算法起始21435的生成。
遍曆法
文献[2]给出一种常数时间的错排生成算法，其本质属于遍曆法，下面以n=5为例说明其算法：
第一步：将最后一位数移至第一位，其余的数顺次向后移动，产生错排d。
如：12345→51234。
第二步：考察d的第二个位置，除去第一个位置的数和2不能放在这个位置上，其余均可。
如：51234→51234或53214或54231。
考察d的第三个位置，除去第一、第二个位置上的数和3不能放在这个位置上，其余的数都可以。
如：51234→51234→51234或51432
51234→53214→53214或53124或53412
51234→54231→54231或54132
以此类推，n个数的错排一直考察到第n个位置为止，结束第二步。
第三步：重複第一、第二步的过程，循环这个程式。
如：12345→51234→45123→34512→23451。
这个循环过程直到第一步产生234⋯(n-1)(n)1，继续执行第二、三步，然后结束。
在算法实现上，生成每一个排列採用无循环处理，时间複杂度为O(1)，因此生成所有错排的时间複杂度为
。
性能分析
上面详述了四种算法思想和流程，下面给出各算法的複杂度分析和性能比较。
对于递归法，n个元素的错排方案数为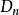
，每个错排均需遍历到，因此基本複杂度为
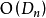。递归函式其中有n次循环，若不考虑错排规则，则每次循环均调用递归函式，考虑错排规则时调用次数满足
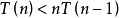，因此
。但由于递归函式的调用开销是很大的，系统要为每次函式调用分配存储空间，并将调用点压栈予以记录。而在函式调用结束后，还要释放空间，弹栈恢复断点。所以，考虑函式处理过程，整体看来，递归法的效率并不高。
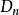
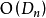
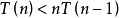
对于基于字典序的筛选法，字典序法的複杂度为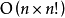
，对每个排列检验其是否为错排的複杂度为
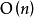，因此该算法的时间複杂度为
。
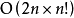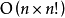
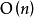
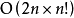
对于改进字典序法，由于其相对基于字典序的筛选法的优点，所以複杂度必然会降低。由于算法中逻辑判断与处理很多，分析其複杂度非常困难。但由于其跳过了大部分的非错排，因此複杂度大约为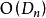
。因此，改进字典序法和文献[2]提出的方法的複杂度大体相同。
综合上述分析可见，算法总体效率大致为：改进字典序法≈文献[2]方法>基于字典序的筛选法>递归法。下面根据数值实验结果给出各算法的性能比较。
表 各算法运行耗时比较（单位：ms）
算法 | n=9 | n=10 | n=11 | n=12 | n=13 |
改进字典序法 | 5 | 44 | 468 | 5534 | 69704 |
文献[2]方法 | 5 | 51 | 553 | 6552 | 83087 |
筛选法 | 8 | 84 | 1050 | 13553 | 181979 |
递归法 | 21 | 186 | 2067 | 25243 | 334661 |
表1给出了各算法运行耗时比较，图4给出了运行时间随n变化的对数曲线图。从上述结果可知，改进字典序法和文献[2]方法的性能相当，前者稍好一些。这两种算法的运行耗时大约为基于字典序的筛选法的一半，而筛选法的运行耗时大约为递归法的一半。注意：由于所取n值在10附近，且曲线纵坐标取log10(t)，因此所得结果大致为直线，只能说明n取10左右时，曲线局部为近似直线，并不说明整体都成此特性。总之，数值实验分析结果与上述时间複杂度分析结果一致。此外，改进字典序法具有最好的算法性能。
原始码
递归实现
void Recursion(int x){ if (x > n) { num_r++; for (int i = 1; i <= n; i++)//输出每一个错排 printf("%d ",dearr_r[i]); printf("\n"); return; } for (int i = 1; i <= n; i++) { if (occup_r[i] == 0 && x != i) //x指安排第x个位置 { occup_r[i] = 1; //vis[i]记录i是否已经被安排 dearr_r[x] = i; Recursion(x + 1); occup_r[i] = 0; //回退，撤销安排的i } }}基于字典序实现
int LexiOrder(int n){ int num_l = 0; bool Flag = true; int *seq = new int[n]; for (int i = 0; i < n; i++) seq[i] = i + 1; num_l++; for (int i = 0; i < n; i++) { if (seq[i] == i + 1) { num_l--; Flag = false; break; } } if (Flag) { for (int i = 0; i < n; i++)//输出每一个错排 printf("%d ",seq[i]); printf("\n"); } for (int i = n - 2; i >= 0;) { if (seq[i] < seq[i+1]) { for (int j = n - 1;j >= 0; j--) { if (seq[j] > seq[i]) { int tmp = seq[i]; seq[i] = seq[j]; seq[j] = tmp; for (int k1 = i + 1, k2 = n - 1; k1 < k2; k1++, k2--) { int tmp = seq[k1]; seq[k1] = seq[k2]; seq[k2] = tmp; } num_l++; Flag = true; for (int i = 0; i < n; i++) { if (seq[i] == i + 1) { num_l--; Flag = false; break; } } if (Flag) { for (int i = 0; i < n; i++)//输出每一个错排 printf("%d ",seq[i]); printf("\n"); } i = n - 2; //重新从右边开始 break; } } } else i--; } delete []seq; return num_l;}改进字典序法实现
int AdLxOrder(int n){ int num_a = 0; int *dearr = new int[n + 1]; int *occup = new int[n + 1]; int Flag = n + 1; //记录不满足错排的元素位置，均满足则为n+1 for (int i = 0; i <= n; i++){ dearr[i] = 0;occup[i] = 0;} for (int i = 1, len = 0; i <= n + 1; i++) { if (i < n) //安排第i个位置 { for (int j = 1; j <= n; j++) //安排第i个位置 { if (occup[j] == 0 && j != i) { occup[j] = 1; //occup[j]记录j是否已经被安排 dearr[i] = j; //安排dearr[i] break; } } } else if (i == n) //安排最后一位 { for (int j = 1; j <= n; j++) //安排第i个位置，无论是否满足 { if (occup[j] == 0) { occup[j] = 1; //occup[j]记录j是否已经被安排 dearr[i] = j; if (j == i) Flag = n; break; } } } else //i == n+1 { if (Flag == n + 1) //满足，输出，并找字典序下一个 { num_a++; for(int k = 1;k <= n; k++) printf("%d ",dearr[k]); printf("\n"); int pos = 0; for (int k = n; k > 1; k--) //从右往左找下降 { if (dearr[k - 1] < dearr[k]) { pos = k - 1; for (int m = n; m > pos; m--) { if (dearr[m] > dearr[pos]) //找到后缀中较大的最小元素 { if (dearr[m] == pos) Flag = pos; //记录不满足的位置 int tmp = dearr[m]; //交换 dearr[m] = dearr[pos]; dearr[pos] = tmp; //记录不满足的位置（只记录最左侧） for (int k1 = pos+1, k2 = n; k1 < k2; k1++, k2--) { if (dearr[k1] == k2 && Flag > k2) Flag = k2; //记录不满足的位置 if (dearr[k2] == k1 && Flag > k1) Flag = k1; //记录不满足的位置 int tmp = dearr[k2]; //陆续交换 dearr[k2] = dearr[k1]; dearr[k1] = tmp; } i = n; //循环末尾有i++，此处特取n break; } } break; } } } else //找关键位置的下一个值 { //关键位置：下降位置和不满足位置的最左者 int pos = 0; for (int k = n; k > 1; k--) //从右往左找下降 { if (dearr[k - 1] < dearr[k]) { pos = k - 1; if (pos > Flag) //pos取下降位置和不满足位置的最左者 pos = Flag; for (int m = pos; m <= n; m++) occup[dearr[m]] = 0; //全部重置 for (int m = dearr[pos] + 1; m <= n; m++) //从dearr[pos]+1开始找 { if (occup[m] == 0 && m != pos) //给pos找到下一个值 { dearr[pos] = m; occup[m] = 1; i = pos; Flag = n + 1; break; } } if (Flag == n + 1) break; else k = pos + 1; //重新向前找下降，循环末尾有k--，此处特+1 } } } } } delete []dearr; delete []occup; return num_a;}